-
Shopping cart
(0)
You have no items in your shopping cart.
Blog archive
Thursday, May 3, 2018
Pythagorean Theorem
The theorem states that:
"The square on the hypotenuse of a right triangle is equal to the sum of the squares on the two legs" (Eves 80-81).
This theorem is talking about the area of the squares that are built on each side of the right triangle.
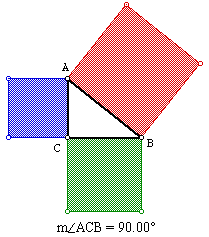
Accordingly, we obtain the following areas for the squares, where the green and blue squares are on the legs of the right triangle and the red square is on the hypotenuse.
area of the green square is ![]()
area of the blue square is ![]()
area of the red square is ![]()
From our theorem, we have the following relationship:
area of green square + area of blue square = area of red square or
Pythagoras' Proof
"Let a, b, c denote the legs and the hypotenuse of the given right triangle, and consider the two squares in the accompanying figure, each having a+b as its side. The first square is dissected into six pieces-namely, the two squares on the legs and four right triangles congruent to the given triangle. The second square is dissected into five pieces-namely, the square on the hypotenuse and four right triangles congruent to the given triangle. By subtracting equals from equals, it now follows that the square on the hypotenuse is equal to the sum of the squares on the legs" (Eves 81).
Consider the following figure.
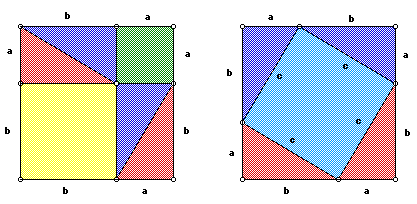
The area of the first square is given by (a+b)^2 or 4(1/2ab)+ a^2 + b^2.
The area of the second square is given by (a+b)^2 or 4(1/2ab) + c^2.
Since the squares have equal areas we can set them equal to another and subtract equals. The case (a+b)^2=(a+b)^2 is not interesting. Let's do the other case.
4(1/2ab) + a^2 + b^2 = 4(1/2ab)+ c^2
Subtracting equals from both sides we have
concluding Pythagoras' proof.
Bhaskara's First Proof
Bhaskara's proof is also a dissection proof. It is similar to the proof provided by Pythagoras. Bhaskara was born in India. He was one of the most important Hindu mathematicians of the second century AD. He used the following diagrams in proving the Pythagorean Theorem.
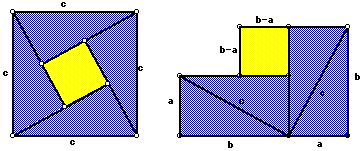
In the above diagrams, the blue triangles are all congruent and the yellow squares are congruent. First we need to find the area of the big square two different ways. First let's find the area using the area formula for a square.
Thus, A=c^2.
Now, lets find the area by finding the area of each of the components and then sum the areas.
Area of the blue triangles = 4(1/2)ab
Area of the yellow square = (b-a)^2
Area of the big square = 4(1/2)ab + (b-a)^2
= 2ab + b^2 - 2ab + a^2
= b^2 + a^2
Since, the square has the same area no matter how you find it
A = c^2 = a^2 + b^2,
concluding the proof.
Bhaskara's Second Proof of the Pythagorean Theorem
In this proof, Bhaskara began with a right triangle and then he drew an altitude on the hypotenuse. From here, he used the properties of similarity to prove the theorem.

Now prove that triangles ABC and CBE are similar.
It follows from the AA postulate that triangle ABC is similar to triangle CBE, since angle B is congruent to angle B and angle C is congruent to angle E. Thus, since internal ratios are equal s/a=a/c.
Multiplying both sides by ac we get
sc=a^2.
Now show that triangles ABC and ACE are similar.
As before, it follows from the AA postulate that these two triangles are similar. Angle A is congruent to angle A and angle C is congruent to angle E. Thus, r/b=b/c. Multiplying both sides by bc we get
rc=b^2.
Now when we add the two results we get
sc + rc = a^2 + b^2.
c(s+r) = a^2 + b^2
c^2 = a^2 + b^2,
concluding the proof of the Pythagorean Theorem.
Garfield's Proof
The twentieth president of the United States gave the following proof to the Pythagorean Theorem. He discovered this proof five years before he become President. He hit upon this proof in 1876 during a mathematics discussion with some of the members of Congress. It was later published in the New England Journal of Education.. The proof depends on calculating the area of a right trapezoid two different ways. The first way is by using the area formula of a trapezoid and the second is by summing up the areas of the three right triangles that can be constructed in the trapezoid. He used the following trapezoid in developing his proof.
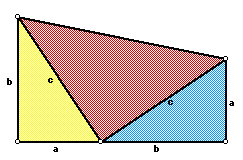
First, we need to find the area of the trapezoid by using the area formula of the trapezoid.
A=(1/2)h(b1+b2) area of a trapezoid
In the above diagram, h=a+b, b1=a, and b2=b.
A=(1/2)(a+b)(a+b)
=(1/2)(a^2+2ab+b^2).
Now, let's find the area of the trapezoid by summing the area of the three right triangles.
The area of the yellow triangle is
A=1/2(ba).
The area of the red triangle is
A=1/2(c^2).
The area of the blue triangle is
A= 1/2(ab).
The sum of the area of the triangles is
1/2(ba) + 1/2(c^2) + 1/2(ab) = 1/2(ba + c^2 + ab) = 1/2(2ab + c^2).
Since, this area is equal to the area of the trapezoid we have the following relation:
(1/2)(a^2 + 2ab + b^2) = (1/2)(2ab + c^2).
Multiplying both sides by 2 and subtracting 2ab from both sides we get
concluding the proof.